随机过程和马尔可夫链

游戏中经常出现暴击率递增的实现方法，那么怎么计算它的期望呢？

Note

• https://en.wikipedia.org/wiki/Markov_chain
• https://www.bilibili.com/video/BV14y4y1S7ve?vd_source=796139b42b923237a89bd18f2217a4e7&spm_id_from=333.788.videopod.sections
• (上面的视频用的PDF)http://dl.nemoudar.com/Introduction-to-Stochastic-Processes-with-R.pdf

背景

视频简介里描述了一种“暴击率递增”的出伤方式，想起了游戏中经常出现的“暴击率递增”概率方案。突然就想计算一下数学期望。

马尔可夫链

马尔可夫过程可以用以下图来表示：

用一种更为形象的方式来表现。在决定吃什么的时候：每次吃过一种之后，下次吃某一种的概率。有下图：

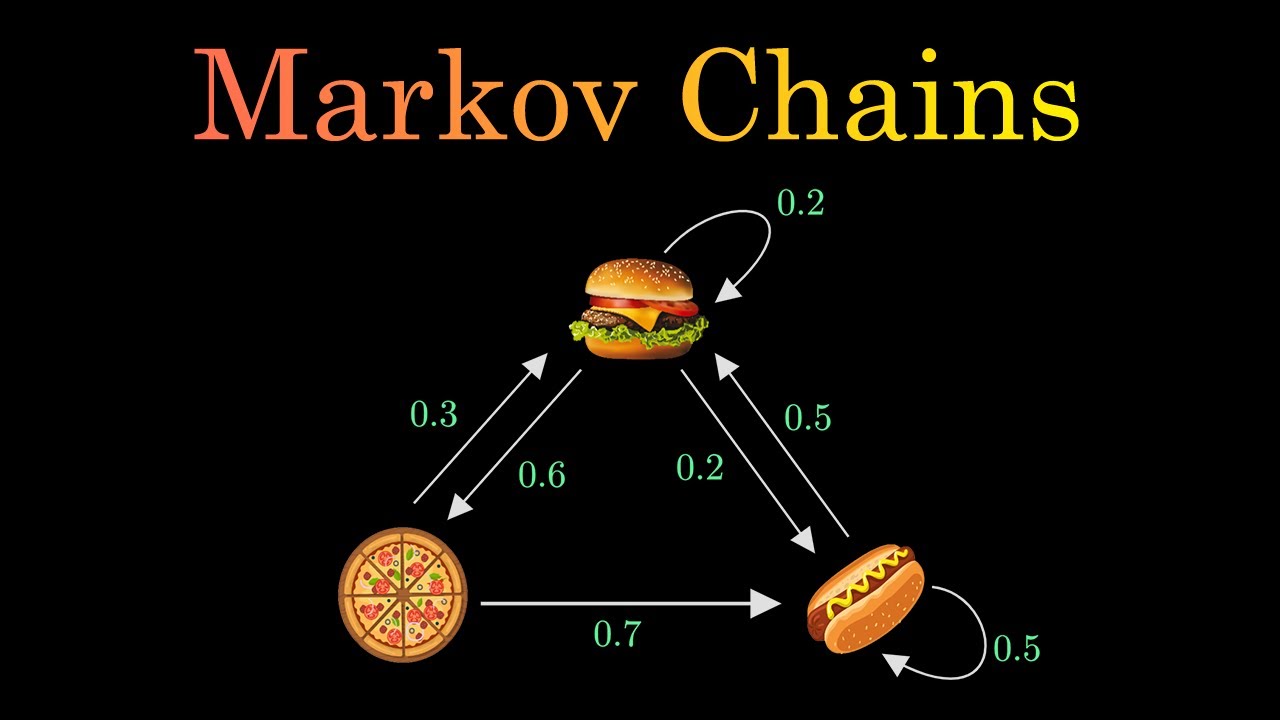
牙膏问题

大概理解了上面的图之后，接着我们用下面的例子来尝试求解。

牙膏问题

假定某大学有1万学生，每人每月用1支牙膏，并且只使用“中华”牙膏与“黑妹”牙膏两者之一。根据本月（12月）调查，有3000人使用黑妹牙膏，7000人使用中华牙膏。又据调查,使用黑妹牙膏的3000人中，有60％的人下月将继续使用黑妹牙膏，40％的人将改用中华牙膏； 使用中华牙膏的7000人中， 有70％的人下月将继续使用中华牙膏，30％的人将改用黑妹牙膏。据此，可以得到如表所示的统计表。

拟用	黑妹牙膏	中华牙膏
现用
黑妹牙膏	60%	40%
中华牙育	30%	70%

计算下个月的两种牙膏的使用情况

这个问题的解很快：

\[ \begin{align*} (3000,7000)\cdot \begin{pmatrix} 0.6 & 0.4 \\ 0.3 & 0.7 \end{pmatrix} = (3900,6100) \end{align*} \]

同样，我们可以求出\(n\)个月之后的用户分布情况：

\[ \begin{align*} y = (3000,7000)\cdot \begin{pmatrix} 0.6 & 0.4 \\ 0.3 & 0.7 \end{pmatrix} ^n \end{align*} \]

借用知乎上对于这个问题的相关讨论， 令P为上面的转移矩阵。根据一系列定理(1)，\(\lim_{n \to \infty} P^n\)存在。 因此，当\(x\)足够大时，\(P^n=P^{n+1}\)，此时，两边同时左乘向量\(x\)，同时令\(\pi=xP^n\)， 得到方程\(\pi \cdot P = \pi\)，因此解该方程即可得到稳态解。

1. 关于这方面的讨论放在wiki里

注意这里，对方程\(\pi \cdot P = \pi\)两边同时转置，\(\pi\)变为列向量，整个方程正是求\(P.T\)的特征值为1的特征向量。 我们很快就能求得上面的方程解为\((3,4)\)，归一化后得到\((0.43,0.57)\)，也就是说两种牙膏的用户比例会趋近0.43:0.57

暴击伤害问题

我们回到上面视频里的伤害计算问题，这里取值与视频不同

假设起始概率为0.2，步长为0.2，则 转移概率矩阵\(P\)为:

\[ \begin{pmatrix} 0.2 & 0.8 & 0 & 0 & 0 \\ 0.4 & 0 & 0.6 & 0 & 0 \\ 0.6 & 0 & 0 & 0.4 & 0 \\ 0.8 & 0 & 0 & 0 & 0.2\\ 1.0 & 0 & 0 & 0 & 0 \end{pmatrix} \]

求解\(\pi\),使得：

\[ \begin{align*} \pi \cdot P = \pi \\ 1^T \cdot \pi = 1 \end{align*} \]

这一次我们使用Python的numpy来计算：

import numpy as np

y = np.array([[0.2, 0.8, 0,   0,   0  ],
              [0.4, 0,   0.6, 0,   0  ],
              [0.6, 0,   0,   0.4, 0  ],
              [0.8, 0,   0,   0,   0.2],
              [1,   0,   0,   0,   0  ]])

# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(y.T)

# 找到特征值为 1 的特征向量
index = np.where(np.isclose(eigenvalues, 1))[0][0]

steady_state = eigenvectors[:, index]
print("稳态分布 L:", steady_state)

# 归一化
steady_state = steady_state / np.sum(steady_state)

print("稳态分布 L:", steady_state)

最后得到稳态分布 L:(0.39834289, 0.31867431, 0.19120459, 0.07648184, 0.01529637)

知乎中这样的计算是不对的！

取\(\pi_0\)计算，得到\(1\cdot (1-p)+p\cdot 2 = 1.273208\)

正确的期望的计算

来自yangzhang同学给出了该问题的数学期望的完整解答，再次感受到我本人的在这方面知识的不足。
首先，将其分为两个空间：概率空间\(x(t)\)和输出空间y(t)，这里暴伤为20:

\[ X=\{0.2,0.4,0.6,0.8,1.0\},Y=\{1,2\} \]

自此状态应该是离散的，并不受前置状态影响的，每个时点只有两个状态：

• 发生暴击，伤害为2
• 没发生暴击，伤害为1

此时稳态伤害期望应为(from yangzhang's)：

\[\begin{aligned} &\mathbb{E}(y_\infty)\\\\ = &\mathbb{E}\left(\mathbb{E}(y_\infty\mid x_\infty)\right)\\\\ = &\sum_{i=0}^4\mathbb{E}(y_\infty\mid x_\infty=X[i])\cdot \mathbb{P}(x_\infty = X[i])\\\\ = &\sum_{i=0}^4(2X[i]+1(1-X[i]))\cdot \pi[i]\\\\ = &\left(2\cdot\begin{bmatrix}.2&.4&.6&.8&1\end{bmatrix}+1\cdot\begin{bmatrix}.8&.6&.4&.2.&0\end{bmatrix}\right) \cdot \pi\\\\ = &\begin{bmatrix} 1.2&1.4&1.6&1.8&2 \end{bmatrix}\begin{bmatrix} 0.39834289\\\\ 0.31867431\\\\ 0.19120459\\\\ 0.07648184\\\\ 0.01529637\\\\ \end{bmatrix}\\\\ = &1.3983429 \end{aligned}\]

后话

再次感谢yangzhang同学对该问题的解答。从这个问题也引申出两个问题：

• 上面的问题的解释表达式是什么
• 在计算机上如何实现真正的随机

第一个问题其实意义不大，第二个问题现在也有人在研究，我打算在后面探讨一下第二个问题

评论